Случалось ли вам закончить трассу, пройдя ее вроде бы удачно и красиво, и обнаружить, что время — намного больше того, на что вы рассчитывали? Возможно, что вы недостаточно эффективно выбрали траекторию движения собаки и потеряли на этом.

В системе управления Грега Дерретта одной из главных целей стоит наиболее эффективная траектория движения собаки. Выбор более быстрого поворота там, где есть альтернатива, очень важен, если вы ставите целью борьбу за время или победу. Возможно, вам регулярно удается пройти чисто, но медленно. Или вы бежите в финале национального чемпионата и хотите выиграть. В любом случае, принятие правильного решения — жизненно важно.

Здесь мы обсуждаем основные факторы, участвующие в расчете траектории собаки, когда вы выбираете, направо ее повернуть или налево после препятствия.

Для начала давайте поговорим об исключении нескольких критериев. Некоторые спортсмены основывают свой выбор исключительно на них. Это 1) Какой маневр я тут буду использовать? 2) Как насчет вон той ловушки?

Если вы хотите выиграть класс и основываетесь только на этих факторах, и делаете выбор в пользу более медленной траектории, есть шанс, что найдется спортсмен, который выберет более короткий путь. Так что при теоретическом расчете быстрейшей траектории не принимайте во внимание управление и ловушки.

Остаются три фактора для использования расчета. Мы рассмотрим их отдельно друг от друга.

№1. Откуда собака приходит на снаряд?

Первый фактор в расчете — спросите себя, откуда собака подходит к препятствию, после которого находится спорное место. При рассмотрении этого мы берем теоретическую линию подхода (в примерах будут использоваться барьеры, поскольку в основном проблемы возникают именно на них). Чтобы ответить на этот вопрос, просто встаньте в точке отталкивания предыдущего снаряда лицом к спорному препятствию. Это приблизительно покажет угол, под которым собака будет приближаться к барьеру. вы получили ответ. Например, на рис.1 барьер 13 — «спорный», вы можете вывернуть собаку и влево, и вправо. Так что встаньте в точке отталкивания на барьер 12. По схеме здесь выигрывает поворот налево.

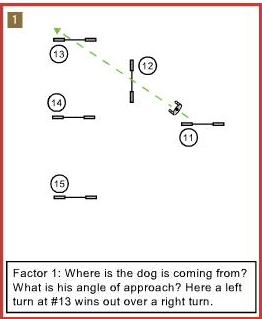
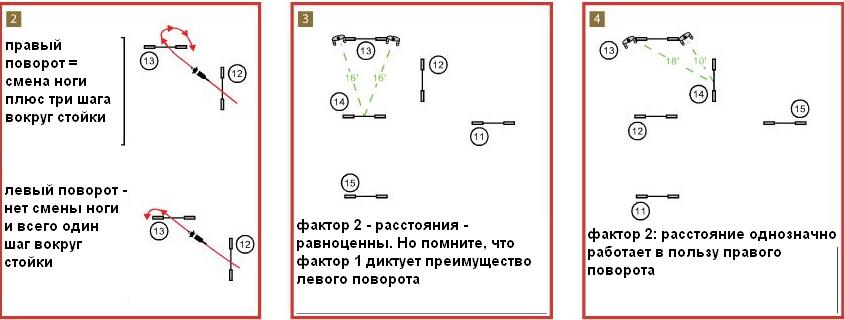
Почему важен угол подхода к спорному барьеру? Когда собаку просят повернуться в противоположную сторону, ей сначала надо сменить ведущую ногу. При этом угол поворота вокруг стойки барьера намного больше, чем если бы ее повернули по ходу движения. Если собаке можно повернуть по ходу движения, ей не надо менять ногу, а стойку обходить ей гораздо меньше. В целом, независимо от размера, те собаки, которых повернут по ходу движения, приземлятся и уже на следующем шаге закончат поворот. Собаки же, которых повернут в противоположную сторону, сделают три-четыре шага после приземления, чтобы обойти стойку и закончить поворот. Больше шагов = больше времени. Так что чем труднее поворачивать, тем больше времени будет потрачено. Рис.2 показывает шаги усредненной собаки.

№2. Какое расстояние от каждой стойки спорного барьера до точки отталкивания на следующее препятствие?

Второй фактор — относительно прост и касается расстояния. Чтобы ответить на этот вопрос, просто промеряйте шагами траектории — от одной стойки спорного барьера до середины следующего барьера. Развернитесь и отсчитайте шаги обратно к другой стойке. Меньшее число и будет вашим ответом.

На рис.3 расстояние одинаково. Но помните, что после первого пункта лидирует левый поворот. Однако на связке на рис.4 собака подходит к спорному барьеру (13) по прямой, так что первый фактор не работает. Но зато расстояние однозначно диктует выбор правого поворота.

№3. Куда двинется собака после спорного барьера?

Последний фактор для рассмотрения — линия движения собаки ПОСЛЕ барьера. Чтобы определить ее, встаньте у каждой стойки спорного барьера и нацельтесь на следующее препятствие. Важно не просто посмотреть на него, но и учесть линию движения по всей связке. Это может оказаться трудным, поскольку выбор одного поворота даст возможность более прямой (=более быстрой) траектории на несколько препятствий, а другого — может привести к нескольким ненужным дугам. Помните, что каждый поворот замедляет движение собаки.

На рис.1 и 3 у нас была прямая после спорного барьера, так что фактор 3 не влиял на принятие решения. Поскольку повороты были равны и при рассмотрении второго фактора, левый поворот выигрывает за счет первого фактора.

Однако то, куда собака пойдет потом, ясно показывает разницу между левым и правым поворотом
на 3 барьере. Если собака поворачивает налево, ей придется сделать поворот еще и на 5. Если она пойдет через право, то у нее получится прямая линия на следующий барьер, что даст выигрыш во времени.

Рис.5 показывает другую связку. Спорный барьер — №3. Левый и правый повороты равны по
первым двум факторам: 1) откуда собака приходит (потому что она приходит с прямой) и 2) расстояние до толчка на следующий барьер равное в обоих случаях. Однако третий фактор показывает, что разница все же есть. Если собака повернет налево, ей нужно будет сделать еще один поворот перед пятым барьером. Но если направо — получится прямая траектория с 3 на 5, что сэкономит массу времени.

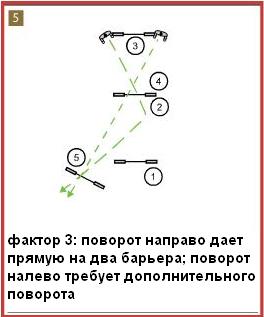
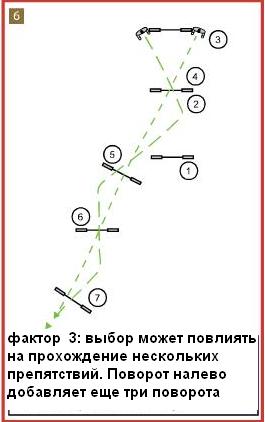
Рис.6 показывает, как линия собаки после спорного барьера может повлиять на прохождение нескольких препятствий. Выбор левого поворота приведет к большим дугам и очень неэффективен.

Заключение

Теперь у вас есть базовый алгоритм расчета быстрейшей траектории. Попрактикуйтесь — достаньте старые схемы трасс, найдите спорные места,
и задайте себе три вышеперечисленных вопроса. Это поможет вам также понять, насколько эффективно вы делали выбор раньше. Затем начните применять алгоритм на
практике.